6.3  Siacci’s Method 6.3.1  The Change of Independent Variables 

6.3  Siacci’s Method 

Siacci’s appr simplified their solutions.

6.3.1  The Change of Independent Variables 

Siacci introduced the “pseudovelocity” u shown in Figure 6-2 as a new independent variable replacing time t in our previous equations. The pseudovelocity u is a velocity in the direction of the extended bore centerline which would give the correct component v x resolved along the x-axis. Then u and v are related by the equation.

(6.3-1)

Then

(6.3-2)

Also

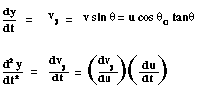(6.3-3) (6.3-4)

 Using equations (6.3-1) through (6.3-4) in equations (6.2-15) and (6.2-16) we can derive the following differential equations of bullet motion in terms of the new independent variable u :

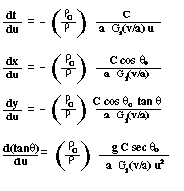(6.3-5) (6.3-6) (6.3-7) (6.3-8)

The initial conditions for the solution of these equations are:

The velocity components v x and v y at any point in the trajectory are given by [equations (6.3-1) and (6.3-3)]:

and the total velocity is

(6.3-11)

We now have a set of first-order differential equations for the time of flight t , the range x , the vertical coordinate y , and the trajectory slope tan X. But these simplified equations of the bullet motion are still nonlinear coupled.